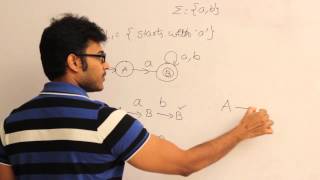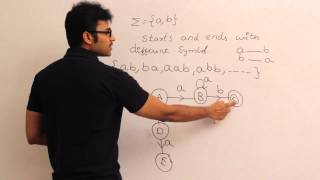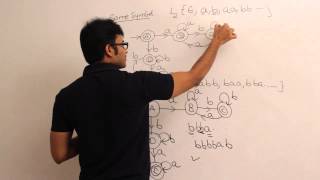The representation theory of triangularizable monoids

Speaker: Benjamin Steinberg Title: The representation theory of triangularizable monoids with applications. Abstract: A finite dimensional algebra over the complex numbers is called basic if its simple modules are 1-dimensional. Every f.d. algebra is Morita equivalent to a unique basic algebra, which in turn can be expressed as a quotient of a path algebra of a finite quiver by an admissible ideal. Thus most of modern representation theory of f.d. algebras assumes that the algebra is basic with a fixed quiver presentation. Recent work of people like Bidigare, Hanlon, Rockmore, Brown, Diaconis, Bjorner, Chung and Graham has exploited the representation theory of a certain class of monoids with basic algebras to analyze finite state Markov chains. On the other hand, motivated by problems in automata theory, the speaker with Almeida, Margolis and Volkov characterized monoids with basic algebras (which we call triangularizable monoids since they are exactly those with a faithful upper triangular matrix representation). The representation theory of these monoids allows the analysis of a much larger class of Markov chains. In this talk we discuss aspects of the representation theory of triangularizable monoids including the classification of simple modules, a basis for the radical, the Cartan invariants and computation of the quiver. Open questions will be raised. Most of this is joint work with Stuart Margolis.