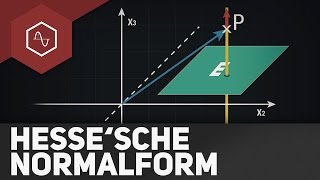
Punkt und Ebene Hesse'sche Normalenform - Gymnasium - Geraden und Ebenen - StrandMathe - Übung 2

Übungshefte zu allen Videos: http://shop.strandmathe.de/ Ist der Normalenvektor (n_0 ) ⃗ einer Ebenengleichung (x ⃗-p ⃗ )∙(n_0 ) ⃗=0 normiert und somit vom Betrag 1, so spricht man von der Hesse’schen Normalenform. Mit dieser lässt sich der Abstand d eines Punktes R(r_1 |r_2 | r_3 ) zur Ebene E bestimmen durch: Unter dem Abstand versteht man die Länge des Lotes, d.h. die senkrechte Verbindung vom Punkt R zur Ebene E. Der Normalenvektor wird wie jeder andere Vektor mit folgender Formel normiert: Auch die Abstandsbestimmung zu einer Ebenen mit der Koordinatengleichung 〖a_1 x〗_1+a_2 x_2+a_3 x_3=b lässt sich zurückführen auf die Hesse’sche Normalenform. Facebook: https://www.facebook.com/strandmathe Instagram: http://instagram.com/strandmathe Twitter: https://twitter.com/strandmathe