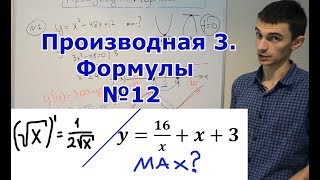Saturday, 17 January, 2026г.
















Где искать: по сайтам Запорожской области, статьи, видео ролики
пример: покупка автомобиля в Запорожье
Нахождение точки максимума функции
Лучшие репетиторы по алгебре в одной базе
http://www.virtualacademy.ru/repetitory/po-algebre/
В данном уроке показывается решение задачи на определение точки максимума заданной функции. Для успешного решения задачи необходимо знать: своего экстремума (минимума или максимума) функция достигает в критических точках, то есть в точках, в которых производная равна нулю или не существует. Сначала, применяя правило дифференцирования, определяется производная функции, которая затем приравнивается к нулю. Разделив обе части полученного уравнения на коэффициент при x, далее оно решается по теореме, обратной теореме Виета. Затем найденные критические точки отмечаются на числовой оси. На каждом из полученных промежутков монотонности определяется знак производной и по этому знаку определяется поведение функции. Если в критической точке функция имеет минимум, то производная меняет знак с минуса на плюс, если максимум - с плюса на минус. Построив для наглядности схематично график функции, определяется точка максимума, что и является ответом.
Приведенное решение можно использовать для результативной подготовки к ЕГЭ по математике, в частности, при решении задач типа B15.
Теги:
егэ в15 алгебра 10 класс производная функции экстремум функции определить знак производной обратная теорема Виета критические точки наибольшее значение функции точка максимума график функции
Похожие видео
Мой аккаунт


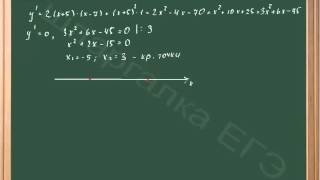 У вашего броузера проблема в совместимости с HTML5
У вашего броузера проблема в совместимости с HTML5