Saturday, 17 January, 2026г.
















Где искать: по сайтам Запорожской области, статьи, видео ролики
пример: покупка автомобиля в Запорожье
Linearity Property of the Laplace Transform and 7 Useful Transforms to Know! Full Example.
In this video we look at the linearity property of Laplace Transforms. It is a common property that is familiar from calculus. The name is derived from the fact that it is satisfied by basic linear functions.
The Linearity property is
L{ af(t) + bg(t)} = aF(s) + bG(s)
This property is use without even thinking about it for derivatives and integrals, and it must become that familiar to you when working with Laplace Transforms as well!
I present seven important transforms to know. Most other transforms can be derived from one of these seven with a translation theorem or other theorem.
There are of course some more complicated transforms that are not derived from these, but they are used less frequently in coursework.
-----------------
My name is Jonathan, and I think Laplace Transforms are incredibly useful when solving differential equations. I hope to share with you, my tips and tricks for working with these tools!
Thanks for watching!
Теги:
Laplace Transforms Linearity of Laplace Transforms Seven Laplace Transforms to Know Linearity Property Linearty for Laplace Transforms Breaking up Laplace Transforms Differential Equations using Laplace Laplace for ODEs Linearity of Laplace Useful Laplace Transforms Useful property of Laplace Transforms
Похожие видео
Мой аккаунт


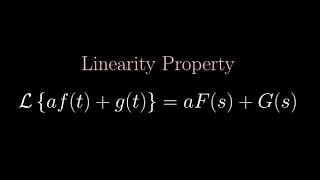 У вашего броузера проблема в совместимости с HTML5
У вашего броузера проблема в совместимости с HTML5


