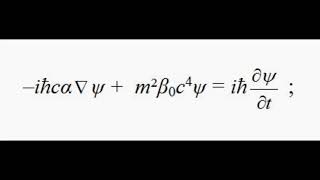Критика формальной физики 3

Сейчас я продемонстрирую парадокс штриха на конкретном примере двух книг: одна из них — известный учебник Ландау и Лифшица "Теория поля", автор второй книги Макс Борн; книга называется "Эйнштейновская теория относительности". Написана она в 20-м году прошлого века, так что на ней выросло не одно поколение физиков-релятивистов. Сейчас при изложении материала я воспользуюсь 6-м разделом курса лекций "Естествознание", выложенного на сайте Sceptic-Ratio. Начнем с учебника Ландау и Лифшица. В нем, как это принято в подавляющем большинстве случаев, через штрихованную систему K' обозначена движущаяся система отсчета, а покоящуюся обозначают через K (без штриха). Читаю вместе с вами: «Пусть в системе K покоится линейка, параллельная оси x, – пишут Ландау и Лифшиц. – Длина ее, измеренная в этой системе, пусть будет Δx = x2 – x1 (x2 и x1 – координаты концов линейки в системе K). Найдем теперь длину этого стержня, измеренную в системе K'. Для этого надо найти координаты обоих концов стержня (x'2 и x'1) в этой системе в один и тот же момент времени t'. Находим (имеются преобразования Лоренца для длины): Собственной длиной стержня называется его длина в той системе отсчета, в которой он покоится. Обозначим ее через l0 = Δx, а длину того же стержня в какой-либо системе отсчета K' – через l. Тогда (4.5) Таким образом, самую большую длину стержень имеет в той системе отсчета, где он покоится. Длина его в системе, в которой он движется со скоростью v, уменьшается в отношении (см. ниже) . Этот результат теории относительности называется лоренцевым сокращением». Теперь смотрим, что пишет Макс Борн по этому же вопросу. «Итак, – пишет Борн, – мы должны определить длину линейки в системе S'(x', ct'), движущейся относительно S(x, ct)... Пусть l0 – длина линейки в системе отсчета S', в которой линейка покоится; l0 называют статической или собственной длиной линейки. Два конца линейки имеют координаты, скажем, x'1 и x'2, так что x'2 – x'1 = l0 . При наблюдении этой линейки из системы S мы по первой из формул (70а) имеем (преобразования Лоренца для координат): (см. ниже фото) (Зачитывается текст из книги Борна) Полагая ..., мы можем записать ... (74). Эта формула утверждает, что длина линейки в системе S оказывается уменьшенной в отношении ... к 1 в точном согласии с гипотезой сокращения, предложенной Фитцжеральдом и Лоренцем». Выражение (74). Таким образом, Ландау – Лифшиц вывели формулу для лоренцева сокращения из прямых преобразований, а Борн – из обратных. То есть, выражения (4.5) и (74) в приведенных текстах только внешне выглядят одинаково, фактически они противоположного свойства. Выражения (4.5) и (74) только внешне выглядят одинаково, фактически они противоположного свойства. Люди гуманитарного склада ума, например, философы и журналисты, будут спорить до хрипоты, обсуждая запутанные тексты обеих книг. Но математику и программисту, имеющему дело с компьютером, разобраться в них ничего не стоит. Они еще раз выпишут два одинаковые формулы — (4.5) и (74), а рядом поставят равенства, которые имели в виду авторы, выражая х-координаты через l-отрезки длины. Ландау и Лифшиц приняли: l0 = Δx и l = Δx' , а Борн ввел противоположные обозначения: l0 = Δx' и l = Δx. Противоположные обозначеия. Следовательно, Ландау и Лифшиц получили формулу (5.1), Борн — (5.2): Выражения (5.1) и (5.2) В данном случае абсолютно неважно, как авторы-релятивисты получали выражения (4.5) и (74); важно помнить об одном: штрихованная система — движется, нештрихованная — покоится. В итоге, авторы книг пришли к взаимоисключающему результату.