Extremwertaufgaben (4): Zylinder mit minimaler Oberfläche bei gegebenem Volumen

Eine weitere Extremwertaufgabe: Hier soll man eine Konservendose mit 800 ml Inhalt so designen, dass die Oberfläche (=Blechverbrauch) minimal wird. ** Alle Videos nach Themen sortiert gelistet: http://mathehoch13.de/Youtube-Videos.php ** Facebook-Seite von mathhoch13 (auch für Fragen/Kommentare): https://www.facebook.com/mathehoch13 Inhalt dieses Videos: (0:11) Erklärung der Aufgabenstellung. Hierbei ergibt sich, dass die Form der Schachtel von dem Abstand x abhängt, mit dem man das rechteckige Stück Pappe vom Rand her umknickt. (0:49) Schritt 1: Welche Größe soll extremal werden? - Antwort: Die Oberfläche der zylindrischen Dose soll minimal werden; Herleitung der Gleichung für die Zylinderoberfläche in Abhängigkeit des Radius r und der Höhe h (2:28) Schritt 2: Nebenbedingung aufstellen, die einen Bezug zwischen den Variablen herstellt; Volumen des Zylinders soll 800 ml = 800 cm^3 betragen. (3:08) Schritt 3: Zielfunktion aufstellen, die nur noch von einer Variablen abhängt (3:46) Schritt 4: Zielfunktion auf Extremwerte untersuchen (6:50) Schritt 5: Prüfen, ob die gefundene Extremstelle in dem durch den Sachzusammenhang gegebenen Definitionsbereich liegt (7:34) Schritt 6: Aufgabenabschluss, d.h.: Überprüfung, ob Randextrema vorliegen, Bestimmung der Abmessungen der Dose mit minimaler Oberfläche. ** Weitere Videos aus der Reihe zu Extremwertaufgaben - 1. Rechteckige Umzäunung mit maximalem Flächeninhalt: https://youtu.be/bujaxU3UPBM - 2. Rechteckige Umzäunung an einer Wand mit maximalem Flächeninhalt: https://youtu.be/waP5WpwAS3Y - 3. Schachtel mit maximalem Volumen: https://youtu.be/YOJnazX2L_w - 4. 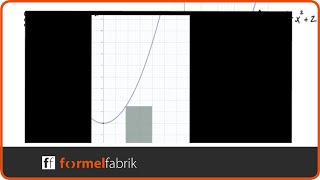Konservendose mit vorgegebenem Volumen bei minimaler Oberfläche: * dieses Video * - 5. Rechteck unter ein Kurve mit maximaler Fläche: https://youtu.be/Pf6n4qfXpIY - 6. Beispiel, warum die Untersuchung der Randextrema so wichtig ist: (Video kommt in Kürze - Abonnieren und nicht verpassen!) ** Videos zu den Ableitungsregeln, die du bis zum Abi beherrschen solltest: - 1. Summenregel/Faktorregel/Potenzregel/Konstantenregel: https://youtu.be/uzjFAApD12w - 2. Kettenregel: https://youtu.be/KU6VsbE8ksw - 3. Produktregel: https://youtu.be/koTr-BEbpdU - 4. Quotientenregel: https://youtu.be/sv6VIp0j-xI Aufruf-ID: m13v0189 ** Hier kannst du meinen Kanal abonnieren und verpasst kein Video mehr: http://www.youtube.com/user/MaNHinDo?sub_confirmation=1 ** Meine Mathe-Facebook-Seite (dort kannst du auch Fragen stellen und Videowünsche posten): https://www.facebook.com/mathehoch13 **Falls Dir meine Videos geholfen haben, freue ich mich immer über :) ein "Like" 8) wenn Du meine Videos mit Mitschülern und Freunden teilst :D Kommentare zu Fragen, Anregungen, Videowünschen :P wenn Du meinen Kanal abonnierst. Alles Gute und bis zum nächsten Mal, Dein Mathe-Coach, Christoph Goemans