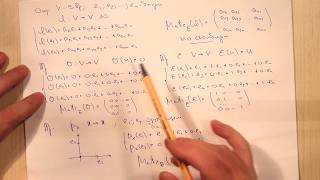Действие линейного оператора в матричной форме. Ответы

Занятия и репетиторство по Skype. Facebook: http://facebook.com/matan.channel , ВКонтакте: http://vk.com/matan.channel , Viber: +7 (927) 74-69-502, WhatsApp: +7 (927) 74-69-502. Как из более простых операторов получать более сложные операторы в матричной форме. -------------------------- Симметрии относительно осей — это два преобразования, которые считаются основными, и матрицы которых мы знаем. Но симметрия относительно наклонной прямой таковой не является, и ее матрица нам не известна. Для того, чтобы преодолеть эту трудность, оператор симметрии относительно наклонной прямой можно представить в виде произведений трех операторов: 1. сначала плоскость поворачивается так, чтобы ось симметрии совпала с горизонтальной осью, 2. затем производится симметрия относительно горизонтальной оси, 3. и наконец, плоскость возвращается на место за счет обратного поворота. -------------------------- В случае необходимости, просмотрите тему «Действие линейного оператора в матричной форме» еще один раз, после чего еще раз вернитесь к тем заданиям видео «Действие линейного оператора в матричной форме», с которыми вы не справились. Обязательно добейтесь того, чтобы эти задачи не вызывали у вас затруднений. -------------------------- Тема «Действие линейного оператора в матричной форме»: https://youtu.be/Ca0pL_fyQ9Y Вопросы по теме «Действие линейного оператора в матричной форме»: https://youtu.be/DgLKLq0FtwA Ответы на вопросы по теме «Действие линейного оператора в матричной форме»:https://youtu.be/moNRKdMHQto