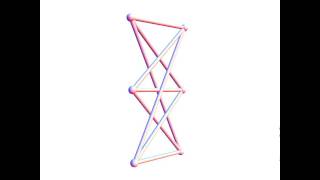
A geometrical proof of the embedding of a non-planar bipartite graph in 3-space without crossings

In graph theory, a planar graph is a graph which can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints. A planar graph already drawn in the plane without edge intersections is called a plane graph or planar embedding of the graph. The Polish mathematician Kazimierz Kuratowski provided a characterization of planar graphs in terms of forbidden graphs, now known as Kuratowski's theorem: "A finite graph is planar if and only if it does not contain a subgraph that is a subdivision of K_5 (the complete graph on five vertices) or K_3,3 (complete bipartite graph on six vertices, three of which connect to each of the other three)." (In the Soviet Union, Kuratowski's theorem was known as the Pontryagin-Kuratowski theorem, as its proof was allegedly first given in Pontryagin's unpublished notes. By a long-standing academic tradition, such references are not taken into account in determining priority, so the Russian name of the theorem is not acknowledged internationally.) This movie shows that while K_3,3 is not a planar graph in the plane, it can be embedded in 3-space without crossings.